Sound & loudness

The human ear is more sensitive to sound in the frequency range 1 kHz to 4 kHz than to sound at very low or high frequencies. Higher sound pressures are therefore acceptable at lower and higher frequencies than in the mid range.
The knowledge about human ear is important in acoustic design and sound measurement. To compensate, sound meters are normally fitted with filters adapting the measured sound response to the human sense of sound. Common filters are

• dB(A)
• dB(B)
• dB(C)

dB(A)

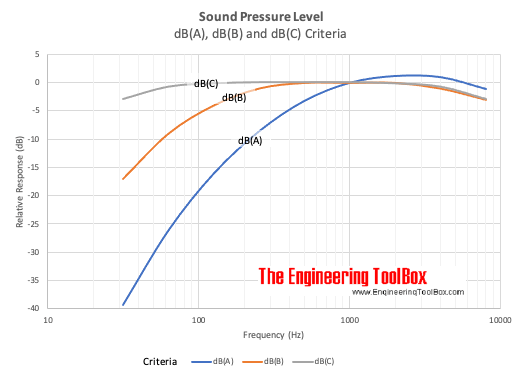
The decibel A filter is widely used. dB(A) roughly corresponds to the inverse of the 40 dB (at 1 kHz) equal-loudness curve for the human ear.
Using the dBA-filter, the sound level meter is less sensitive to very high and very low frequencies. Measurements made with this scale are expressed as dB(A).

dB(B) and dB(C)

The decibel C filter is practically linear over several octaves and is suitable for subjective measurements at very high sound pressure levels. The decibel B filter is between C and A. The B and C filters are seldom used.

Comparing dB(A), dB(B) and dB(C)

The decibel filters A, B and C are compared below:

Relative Response (dB)	Frequency (Hz)
	31.5	63	125	250	500	1000	2000	4000	8000
dB(A)	-39.4	-26.2	-16.1	-8.6	-3.2	0	1.2	1	-1.1
dB(B)	-17	-9	-4	-1	0	0	0	-1	-3
dB(C)	-3	-0.8	-0.2	0	0	0	-0.2	-0.8	-3

Example - Measuring dB(A)

If sound pressure is measured at different octaves the resulting dB(A) sound pressure can be calculated by logarithmic addition.

Octave	1	2	3	4	5	6	7	8
Measured Sound Pressure Level (dB)	54	60	64	53	48	43	39	32
db(A) filter (dB)	26	16	9	4	0	-1	-1	1
Resulting Sound Pressure Level (dB)	28	44	55	49	48	44	40	31

1. Logarithmic adding decibels in octave 4 and 5 gives approximately 51.5 dB.
2. Logarithmic adding decibels in octave 3 together with the sum from 4 and 5 (1) gives approximately 56.5 dB.
3. The resulting sound pressure level in octave 1, 2, 6, 7 and 8 is low compared with (2) and can be neglected.
4. The resulting sound pressure level can therefore be estimated to approximately 57 dB(A)

 

The Definition of Decibel

Decibel is a logarithmic unit used to describe the ratio of the signal level - power, sound pressure, voltage or intensity or several other things.
The decibel can be expressed as:

decibel = 10 log(P / P_ref )         (1)
where
P = signal power (W)
P_ref = reference power (W)

A decibel is one-tenth of a Bel - named after Alexander Graham Bell, the inventor of the telephone.
Note! Doubling the signal level increases the decibel with 3 dB (10 log (2)).
If we know the decibel value and the reference level, the absolute level can be calculated by transforming (1) to:

P = P_ref 10^{(decibel / 10)}         (2)

Example - Sound Intensity and Decibel

The difference in sound intensity of 10^-8 watts/m² and 10^-4 watts/m² (10,000 units) can be calculated in decibels as

ΔL_I = 10 log( (10^-4 watts/m²) / (10^-12 watts/m²) ) - 10 log( ( 10^-8 watts/m²) / ( 10^-12 watts/m²) )
    = 40 dB

Increasing the sound intensity by a factor of

• 10 raises its level by 10 dB
• 100 raises its level by 20 dB
• 1,000 raises its level by 30 dB
• 10,000 raises its level by 40 dB and so on 

•  

   

  Sound Intensity

  Sound Intensity is the Acoustic or Sound Power (W) per unit area. The SI-units for Sound Intensity are W/m².
  

  Sound Intensity Level

  The dynamic range of human hearing and sound intensity spans from 10^-12 W/m² to 10 - 100 W/m². The highest sound intensity possible to hear is 10,000,000,000,000 times as loud as the quietest!
  
  This span makes the absolute value of the sound intensity impractical for normal use. A more convenient way to express the sound intensity is the relative logarithmic scale with reference to the lowest human hearable sound - 10^-12 W/m² (0 dB).
  Note! In US a reference of 10^-13 watts/m² are commonly used.
  The Sound Intensity Level can be expressed as:
  

  L_I = 10 log(I / I_ref)         (1)
  where
  L_I = sound intensity level (dB)
  I = sound intensity (W/m²)
  I_ref = 10^-12 - reference sound intensity (W/m²)
  

  The logarithmic sound intensity level scale match the human sense of hearing. Doubling the intensity increases the sound level with 3 dB (10 log (2)).
  

  Example - Sound Intensity

  The difference in intensity of 10^-8 watts/m² and 10^-4 watts/m² (10,000 units) can be calculated in decibels as
  

  ΔL_I = 10 log( (10^-4 watts/m²) / (10^-12 watts/m²) )
  - 10 log( ( 10^-8 watts/m²) / ( 10^-12 watts/m²) )
  = 40 dB
  

  Increasing the sound intensity by a factor of
  
• 10 raises its level by 10 dB
• 100 raises its level by 20 dB
• 1,000 raises its level by 30 dB
• 10,000 raises its level by 40 dB
• and so on

Note! Since the sound intensity level may be difficult to measure, it is common to use sound pressure level measured in decibels instead. Doubling the Sound Pressure raises the Sound Pressure Level with 6 dB.

Loudness

Sound intensity and feeling of loudness:

• 110 to 225 dB - Deafening
• 90 to 100 dB - Very Loud
• 70 to 80 dB - Loud
• 45 to 60 dB - Moderate
• 30 to 40 dB - Faint
• 0 - 20 dB - Very Faint

Sound Power, Intensity and Distance to Source

The sound intensity decreases with distance to source. Intensity and distance can be expressed as:

I = L_w / 4 π r²         (2)
where
L_w = sound power (W)
π = 3.14
r = radius or distance from source (m)

Sound Intensity and Sound Pressure

The connection between Sound Intensity and Sound Pressure can be expressed as:

I = p² / ρ c         (3)
where
p = sound pressure (Pa)
ρ = density of air (1.2 kg/m³ at 20^oC)
c = speed of sound (331 m/s)

The table below indicates the sound pressure level in decibel caused by some common sources.

Source	Sound Pressure Level (dB)
Threshold of Hearing
Quietest audible sound for persons with excellent hearing under laboratory conditions2)	0
Quietest audible sound for persons under normal conditions
	10
Rustling leaves	20
Noticeably Quit - Voice, soft whisper
Quiet whisper (1 m)	30
Home	40
Moderate
Quiet street	50
Loud - Unusual Background, Voice conversation 1 m
Conversation	60
Loud - Voice conversation 0.3 m
Inside a car Car (15 m) Vacuum cleaner (3 m) Freight Train (30 m)	70
Loud singing	75
Loud - Intolerable for Phone Use
Automobile (10 m) Maximum sound up to 8 hour (OSHA criteria - hearing conservation program) Pneumatic tools (15 m) Buses, trucks, motorcycles (15 m)	80
Motorcycle (10 m)	88
Food blender (1 m) Maximum sound up to 8 hour (OSHA1) criteria - engineering or administrative noise controls) Jackhammer (15 m) Bulldozer (15 m)	90
Subway (inside)	94
Very Loud
Diesel truck (10 m)	100
Lawn mower (1 m)	107
Pneumatic riveter (1 m)	115
Threshold of Discomfort
Large aircraft (150 m over head)	110
Chainsaw (1 m)	117
Deafening, Human pain limit
Amplified Hard Rock (2 m) Siren (30 m)	120
Jet plane (30 m) Artillery Fire (3 m)	130
Short exposure can cause hearing loss
Military Jet Take-off (30 meter)	150